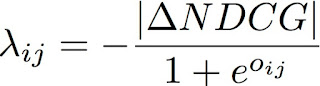ランキング学習勉強会第１回 まとめ
ランキング学習勉強会第１回 まとめ
先月、株式会社ロンウイットにて、ランキング学習勉強会が開催された。私は勉強会の後半で当時まで Learning-to-Rank for Lucene (LTR4L) で実装してきたニューラルネットワーク（NN）のアルゴリズムの理論について発表し、LTR4L のデモも行った。イベントの詳細や登壇者が使用したスライドなどはこちらで見られる。ランキング学習勉強会で紹介したアルゴリズムは以下のとおりである。
- PRank (Perceptron Ranking)
- OAP-BPM
- RankNet
- FRankNet
- LambdaRank
- SortNet
- ListNet
加うるに、以下の点についても解説した。
- 損失関数
- 精度評価指標
- 最急降下法・確率的勾配降下方
- バックプロパゲーション（誤差逆伝播法）
それぞれのアルゴリズムについては LTR4L の README.md でまとめてはあるが、勉強会でより詳細に解説したので、以下 NN のアルゴリズムを簡単にまとめていこうと考えている。
疑似コードは LTR4L の README.md 、または元論文を参照。FRankNet と SortNet の解説は省略する。
単純パーセプトロンのアルゴリズム
PRank (Perceptron Ranking)
種類：ポイントワイズ
PRank は単純パーセプトロンという、入力層と出力層の２層のニューラルネットワークを用いたアルゴリズムであり、その目的は文書を分類することである。
入力層は特徴量分のノードで構造されており、出力層はノード１個（出力ノード）で構造されている。
各入力ノードは出力ノードに重み付きのリンク（Edge）を張られ、出力ノードに信号を送る。
どういう信号を送るかというと、入力信号（特徴）をそのまま出力し、それを重みでかけ、それを出力ノードに入力する。出力ノードは、入力信号の総和をそのまま出力する。
PRank の目的は文書を分類することなので出力に基づいた分類法方が必要である。分類するために、ランキング順位数と同じ数のしきい値を用意する。
例えば、文書につく可能なランキング順位が １☆、２☆、３☆ とした場合はしきい値を３つ用意する。出力を初めて超えるしきい値の番号が予測値（予測クラス・分類）である。
PRank では重み（今後 ω と呼ぶ）としきい値（b）を学習する。重みとしきい値の初期値は (0, 0, 0, ..., 0) と (0, 0, ..., ∞) である。
気づいたかもしれないが、PRank の単純パーセプトロンの出力は単なる内積（ω と文書の特徴量 x の内積）である。
具体的にどうやって重みとしきい値を学習するかというと、現在のモデル（ω、b）で内積を求めて分類した上で ω を x に近づけ、誤った b のみ正解に近づけるのである。
符号に基づいて ω と b を更新する（符号が大きければ重みを大きく変える。符号がなければ更新はしない）。
PRank は簡単かつ実装しやすいアルゴリズムである分、正確なモデルが求められない問題が多い。
それはなぜかというと、PRank では線形非分離な問題を解決できないからである。但し、線形分離可能な問題であれば比較的高速に正確なモデルを求められる。
OAP-BPM (Online Aggregate Prank-Bayes Point Machine)
種類：ポイントワイズ
OAP-BPM は PRank を用いたアルゴリズムであり、その目的は PRank と同様、文書を分類することである。
OAP-BPM は PRank と同様に予測・判定時に文書の特徴と重みの内積を求め、それとしきい値に基づき分類を予測する。
PRank との異なる点は重みとしきい値の更新である。
OAP-BPM では、N個の PRank のインスタンスを持って学習する。１エポックである文書の特徴を各 PRank のインスタンスにユーザーに指定された確率で入力する。
入力した場合は、OAP-BPM の重みとしきい値を以下の式で更新する。
OAP-BPM も比較的簡単かつ実装しやすい。さらに、（少なくとも Microsoft のデータセットで実行した時の）評価を比較すると、OAP-BPM の方がうまく学習できるようでもある。
多層パーセプトロン (Multi-Layer Perceptron, MLP) のアルゴリズム
以下、多層パーセプトロンのアルゴリズムの理論を解説する。
多層パーセプトロンとは、文字通り複数の層で構造されているニューラルネットワークのことである。つまり、入力層と出力層の他に隠れ層がある。
入力層以外、各層の各ノードは出力するために活性関数を用いる。
活性化関数とは、ノードの入力信号の総和を出力に変える関数である。活性化関数は ReLU, Sigmoid など多種類ある。
基本的には隠れ層の数、それらのノード数、そしてノードの活性化関数はユーザーに指定される。
重み更新のルールに関しては、基本的にはバックプロパゲーションを用い、アルゴリズムによってはバックプロパゲーションする頻度や、インスタンスに必要な文書の数（または、バックプロパゲーションに必要な文書の数）が異なる。
また、バックププロパゲーションで最小化しようとする損失関数もアルゴリズムによって異なる。
それぞれのアルゴリズムの主な違いは
- ネットワークの構造（出力数の数・活性化関数など）
- 損失関数
- 更新する頻度
NNRank
種類：ポイントワイズ
NNRank は多層パーセプトロンを用いたアルゴリズムであり、目的は文書を分類することである。
NNRank のネットワークの構造だが、出力ノード数は分類の数 - 1 であり、その活性化関数は Sigmoid である。
NNRank の出力は直接文書を分類しようとする。
以上のイメージを見れば分かるように、NNRank では出力ノードにしきい値があり、しきい値が初めて出力を超えるノードの番号（あるいは番号 - 1）が予測分類・クラスである。
ポイントワイズのアルゴリズムなので文書ごとに重みを更新できる。
重みの更新に必要最低限の手順は以下のとおりである（これを複数の文書で行った上で重みを更新するとミニバッチになる）:
- 文書i で forward propagation
- 文書i のラベル・正解で backpropagation
欠点としては、関連度のようなスコアを得られないので、それが必要な場合は NNRank を用いられないと考える。
RankNet
種類：ペアワイズ（学習時）
多用されており、様々なアルゴリズムのベースとなっている RankNet は多層パーセプトロンを用いたアルゴリズムであり、目的はペアワイズの損失を最小化することである。
要するに二つの文書の中、どちらの方が関連度が高いかを正確に予測するというのが目的だが、出力されるのはは１個の文書関連度のようなスコアである。
RankNet は交差エントロピー誤差という損失関数を最小化しようとし、これを計算するためには二つの文書が必要である。従って、予測するために文書１個しか必要でないにもかかわらず、重みを更新するための必要最低限の手順は以下のとおりである:
- 文書i で forward propagation、 スコア si を得る
- 文書j で forward propagation、sj を得る
- si - sj を用い、backpropagation
- 文書i で forward propagation
- backpropagation (損失関数の対称性で勾配を得られる)
精度は比較的高いが、ペアワイズの損失が下がるからといって必ずしも精度が上がるというわけではない。例えば以下のイメージを見てみよう。
以上のイメージでは、それぞれの線があるクエリでヒットした文書であり、点線は関連している文書としよう（それ以外の文書は関連していない）。
RankNet では、右側の損失の方が低い。要するに、右側の方が誤った文書ペアの数が低い。
だが、例えば NDCG@1 や NDCG@2 で評価すると、左側の方が精度が高い。
「では、直接 NDCG や精度評価指標を最適化・最大化する方法はあるのではないか」という発想から次に解説する LambdaRank が生まれた。
LambdaRank
種類：ペアワイズ（だが、ランクのリストが必要）
RankNet をベースにした LambdaRank も多層パーセプトロンを用いたアルゴリズムであり、目的は精度を直接最適化することである。
LambdaRank では RankNet で用いられた交差クロスエントロピー誤差の損失関数の勾配を改良し NDCG や MRR など精度評価指標を直接最適化する。
RankNet では損失を最小化しても、必ずしも精度があがるわけではないという問題があったのだが、それを解決するために、NDCG を最適化したい場合、以下のように勾配を改良する。
|ΔNDCG| は文書i と文書j を交換した時の NDCG の差分である。
NDCG@1 を見た場合、３位の文書を１位にあげる方が、８位の文書を１位にあげるより効率が良い。従って、以下の式が成り立つ勾配を求める（以下のイメージの ∂C を参照）。
なぜ |ΔNDCG| でかけるかというと、以上の式が成り立つからである。
|ΔNDCG| を計算しなければならないため、クエリに対する文書のリストの情報が必要である。従ってペアワイズでありつつも、リストの情報が必要である。
LambdaRank では損失関数の勾配を直接定義する。従って損失関数そのものがどういう形をしているかは不明である。
だが、損失を最小化・最大化するために損失関数そのものではなく、その勾配が必要であるため、損失関数が不明でも正確なモデルを得られる。
ちなみに、勾配を定義しそれを用いるという手法は、自由に勾配の関数が作れるわけではない。その積分である損失関数は必ず存在しなければならないという条件を満たす必要がある。
ポアンカレの補題を参照。
ListNet
種類：Listwise
ListNet は多層パーセプトロンを用いたアルゴリズムであり、目的はリストワイズの損失を最小化することである。
リストワイズのネットワーク構造は RankNet ど同様であるが、異なる点はエントロピーの損失関数がペアワイズではなく、リストワイズというところである。
RankNet の損失関数では文書i,j で文書i の方が関連度が高い確率を用いるのに対し、ListNet では文書i が１位になる確率を用いる。
